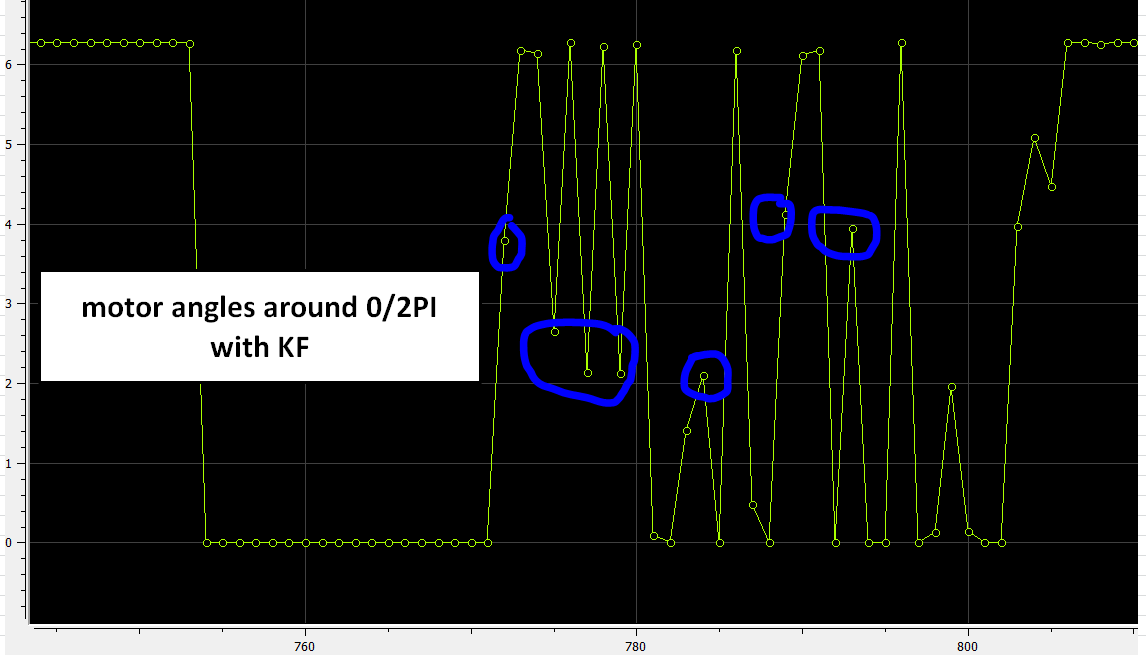
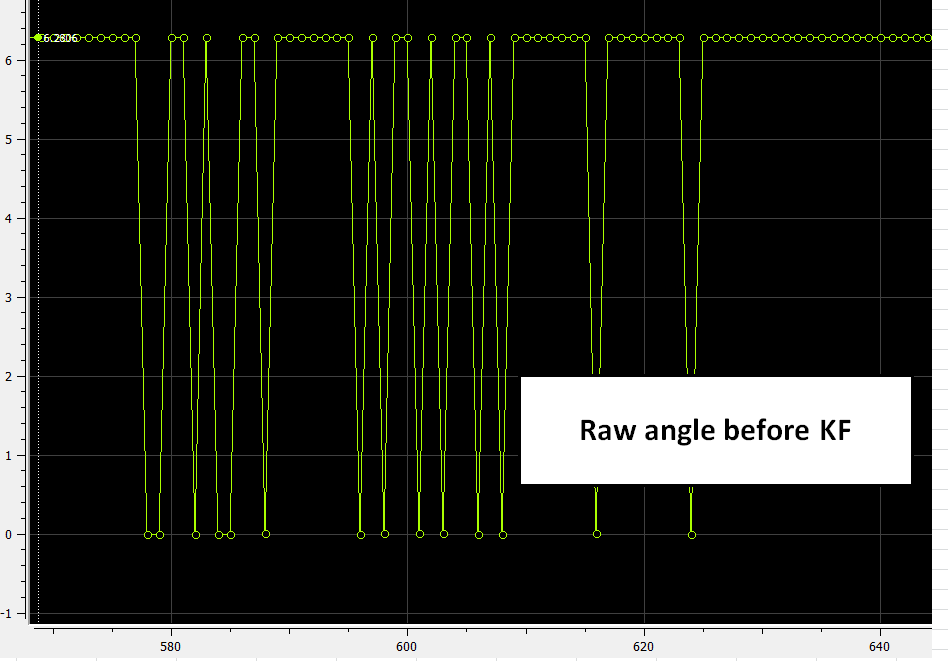
One-dimensional Kalman Filtering for simple, well behaved time series
physical measurements such as angle, temperature, velocity, etc.
This algorithm works by a two-phase process. For the prediction phase, the Kalman filter produces estimates
of the current state variables, along with their uncertainties. Once the outcome of the next measurement
(necessarily corrupted with some error, including random noise) is observed, these estimates are updated
using a weighted average, with more weight being given to estimates with greater certainty.
The algorithm is recursive. It can operate in real time, using only the present input measurements and
the state calculated previously and its uncertainty matrix; no additional past information is required.
The predicted value could be fine-tuned by modifying the error and system noise inputs real-time to achieve optimal results.
This however will require extending the class to monitor error and noise real-time and is a very complex topic.
Fun fact, the first publicly known application was made at NASA Ames Research Center in the early 1960s
during feasibility studies for circumlinear navigation and control of the Apollo space capsule.
The algorithm was implemented in assembler in magnetic core memory on the capsule board navigation module.
Some decent default values: measurement_error = 2; estimation_error = 2; system_noise = 0.01;
Example:
include <KalmanFilter.h>
kalmanFilter KalmanFilter;
float measurement = kalmanFilter.getEstimate(measurement, 2.0, 2.0, 0.01)
class KalmanFilter
{
public:
KalmanFilter();
float getEstimate(float signal_measurement, float measurement_error, float estimation_error, float system_noise);
private:
float previous_estimate = 0.0;
float gain = 0.0;
float signal_estimate = 0.0;
float error_estimate = 0.0;
};
KalmanFilter::KalmanFilter(){};
float KalmanFilter::getEstimate(float signal_measurement, float measurement_error, float estimation_error, float system_noise)
{
if ( error_estimate == 0.0 ) error_estimate = measurement_error;
gain = error_estimate/(error_estimate + measurement_error);
signal_estimate = previous_estimate + gain * (signal_measurement - previous_estimate);
error_estimate = (1.0 - gain)*error_estimate + fabs(previous_estimate-signal_estimate)*system_noise;
previous_estimate=signal_estimate;
return signal_estimate;
}
Please feel free to modify as needed. I did it a bit dirty to take care of the init instead, with the cheat:
if ( error_estimate == 0.0 ) error_estimate = measurement_error;
because I didn’t want to initialize first with default values, and wanted to be able to change the parameters real time, however checking for 0.0 is a bit dangerous.
You can extend
KalmanFilter::KalmanFilter(){};
by creating some body and logic, to handle initialization params, however this will increase the memory footprint.
As they say, caveat emptor.
Edit: I am using it to design a high-torque (many Kg-m) natural movement servo joint, because when you have really heavy payloads the dynamic stress will exceed the bearing capacity, and you need to implement some good filtering coupled with S-curves. The Kalman filter on the target angle does that extremely fast and you can modify the parameters to achieve whatever curve and frequency/error filtering you want with virtually zero memory footprint.