SimpleFOC _sin calculation

[ChrisMicro]

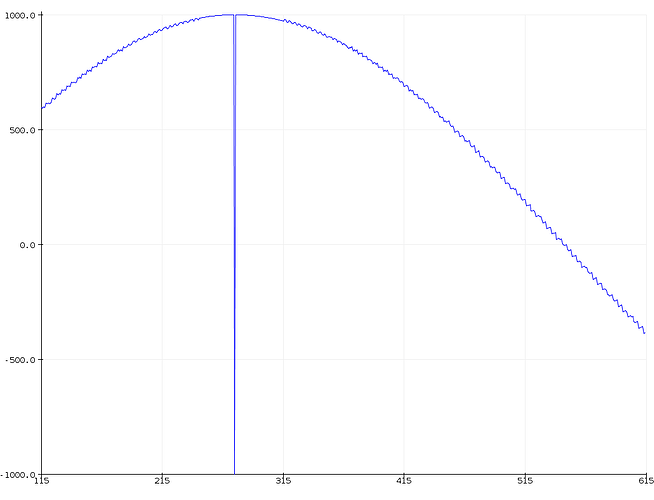
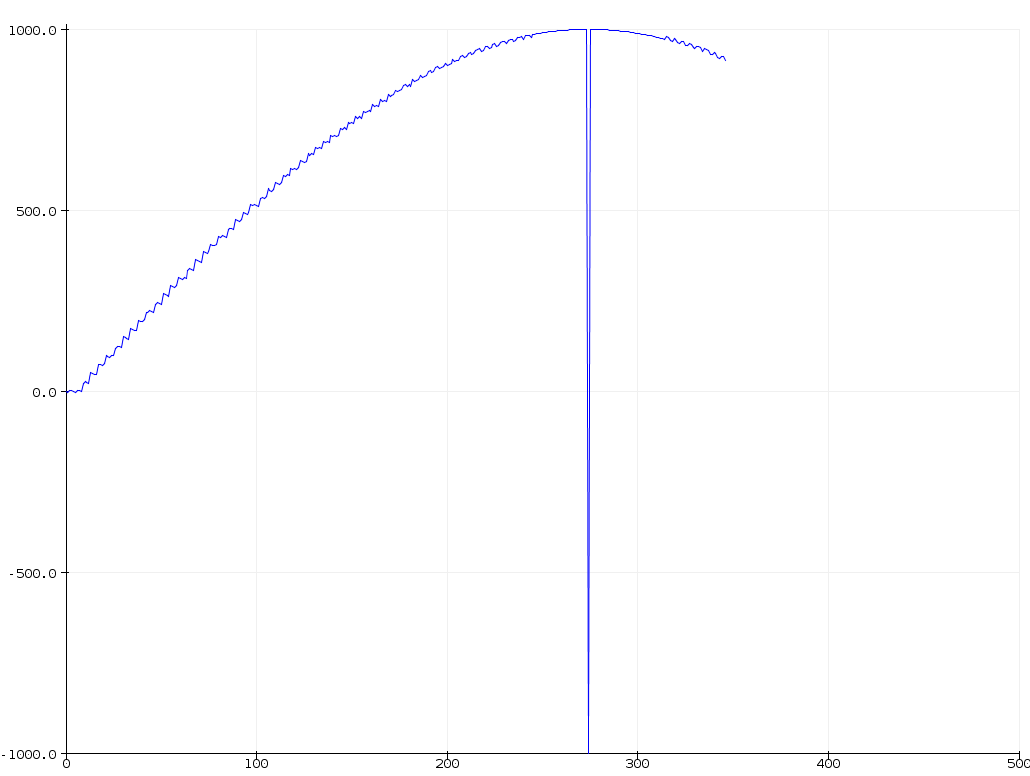
Because I wanted to know how fast the sine wave calculation of SimpleFOC is on an Arduino-Nano, I wrote a test sketch:

/*  
 *   Test the SimpleFoc sine wave function for accuracy and speed
 *   
 *   2024-06-29 ChrisMicro
 *   
 * https://github.com/simplefoc/Arduino-FOC/blob/master/src/common/foc_utils.cpp
 * 
 * 
  */

#define _2PI 6.28318530718f
#define _PI_2 1.57079632679f
// function approximating the sine calculation by using fixed size array
// uses a 65 element lookup table and interpolation
// thanks to @dekutree for his work on optimizing this
__attribute__((weak)) float _sin(float a){
  // 16bit integer array for sine lookup. interpolation is used for better precision
  // 16 bit precision on sine value, 8 bit fractional value for interpolation, 6bit LUT size
  // resulting precision compared to stdlib sine is 0.00006480 (RMS difference in range -PI,PI for 3217 steps)
  static uint16_t sine_array[65] = {0,804,1608,2411,3212,4011,4808,5602,6393,7180,7962,8740,9512,10279,11039,11793,12540,13279,14010,14733,15447,16151,16846,17531,18205,18868,19520,20160,20788,21403,22006,22595,23170,23732,24279,24812,25330,25833,26320,26791,27246,27684,28106,28511,28899,29269,29622,29957,30274,30572,30853,31114,31357,31581,31786,31972,32138,32286,32413,32522,32610,32679,32729,32758,32768};
  unsigned int i = (unsigned int)(a * (64*4*256.0f/_2PI));
  int t1, t2, frac = i & 0xff;
  i = (i >> 8) & 0xff;
  if (i < 64) {
    t1 = sine_array[i]; t2 = sine_array[i+1];
  }
  else if(i < 128) {
    t1 = sine_array[128 - i]; t2 = sine_array[127 - i];
  }
  else if(i < 192) {
    t1 = -sine_array[-128 + i]; t2 = -sine_array[-127 + i];
  }
  else {
    t1 = -sine_array[256 - i]; t2 = -sine_array[255 - i];
  }
  return (1.0f/32768.0f) * (t1 + (((t2 - t1) * frac) >> 8));
}

// function approximating cosine calculation by using fixed size array
// ~55us (float array)
// ~56us (int array)
// precision +-0.005
// it has to receive an angle in between 0 and 2PI
__attribute__((weak)) float _cos(float a){
  float a_sin = a + _PI_2;
  a_sin = a_sin > _2PI ? a_sin - _2PI : a_sin;
  return _sin(a_sin);
}


void setup()
{
  Serial.begin(115200);

}

float angle = 0;

#define BUFLEN 100
float buffer[BUFLEN];

void loop()
{
  const float dphi=2 * PI / 360/3;
  uint32_t start=micros();
  for (int n = 0; n < BUFLEN; n++)
  {
    buffer[n] = _sin(angle);
    //buffer[n] = sin(angle);
    angle += dphi;
  }
  uint32_t dt=micros()-start;
  
  for (int n = 0; n < BUFLEN; n++)
  {
    Serial.println(buffer[n]*1000);
    delay(5);
  }
  /*
  Serial.print("t [us]: ");
  Serial.println(dt/BUFLEN);
  delay(1000);
  Serial.println("*******************");
*/
}

Can it be, that is has interpolation problems?:

[Candas1]

I have not tested this code myself, but have you used any optimization flags ?

[ChrisMicro]

I just run the code above in the Arduino IDE and watching the result in the plotter window. The code should not be dependent on compiler flags.

[dekutree64]

Strange, I tried running that code on PC and there’s no issue at the reversal point. I even tried directly setting the variable i in the _sin function to 16383, 16384, and 16385 and it gives the expected results. The line shouldn’t be stepped like that either, so I suspect some weirdness with the serial plotter. I’ll try it on Arduino and see if I can figure out what’s going on.

EDIT: Yep, testing on Pro Mini (8MHz Atmega328P) I get the blip at pi/2 in the plotter as well, but snapping screenshots of the fast-moving serial monitor does not show any problems. Values at the turnaround point: 999.85, 999.94, 999.97, 999.88, 999.82

[ChrisMicro]

@dekutree64

Strange, I tried running that code on PC and there’s no issue at the reversal point.

Yes, I just compiled and ran it on a PiPico and there seems no problem. Can anyone try the code on an Atmega328 based Arduino? At least on my Arduino-Nano I observe the problem.

[ChrisMicro]

@dekutree64

EDIT: Yep, testing on Pro Mini (8MHz Atmega328P) I get the blip at pi/2 in the plotter as well, but snapping screenshots of the fast-moving serial monitor does not show any problems. Values at the turnaround point: 999.85, 999.94, 999.97, 999.88, 999.82

The blip appears only on the first wave. This might come from the phase accumulator used for the progressing sine wave and the moving match of the interpolation points off the sine calculation. Another observation is the ringing or small steps visible in the screen shot. On the PiPico they are not visible.

Edit:
Meanwhile I think I found the problem:
If I change the integers for the large MCUs (32bit or 64bit PC) to uint16_t and int16_t the problems occur.

  // problematic code: small integer size on small MCUs:

  //unsigned int i = (unsigned int)(a * (64*4*256.0f/_2PI));
  uint16_t i = (uint16_t)(a * (64*4*256.0f/_2PI));
  //int t1, t2, frac = i & 0xff;  
  int16_t t1, t2, frac = i & 0xff;

Rule for professional developers:

NEVER EVER USE BUILTIN INTEGERS !
use always integer types with defined length

wrong: int
right: int8_t, int16_t, int32_t

[dekutree64]

Nice catch! That is a major error on my part. If I recall, I intentionally chose the unspecified width to use whatever is fastest for the CPU it’s compiled for, but neglected two important details to go with it. Specifically, the last table entry should be fudged to 32767 so it won’t overflow signed 16-bit when positive, and the (((t2 - t1) * frac) >> 8) portion of the calculation should always be done in 32-bit, like

return (1.0f/32768.0f) * (t1 + (int)((((int32_t)t2 - t1) * frac) >> 8));

But I would also be ok with changing t1 and t2 to int32_t. It should only be a few more cycles on 16-bit CPUs, and will give exact 1.0 and -1.0 output at pi/2 and 3pi/2 unlike the fudged table. Probably should add explicit casts to int32_t before negating the table values in that case.

I’ll open a github issue for this.

[ChrisMicro]

the last table entry should be fudged to 32767

That’s also what came to my mind. The int16_t integer range goes from -32768 to +32767 and therefore the max entry should be +32767.

The return line should than probably look like

return (1.0f/32767.0f) * (t1 + (int32_t)((((int32_t)t2 - t1) * frac) >> 8));

[ChrisMicro]

Another point is the unclean interpolation on an Atmega328.
This is the result of to small integers for t1,t2

Changing the length to

 int32_t t1, t2;

Solves this problem for the old max value of 32768.

The phase conversion line seems to be problematic for me:

unsigned int i = (unsigned int)(a * (64*4*256.0f/_2PI));

with quite undefined behaviour at large phase values ‘a’.

[dekutree64]

Here is the pull request I made earlier today Fix for #415 sin/cos integer overflow on 16-bit CPUs by dekutree64 · Pull Request #416 · simplefoc/Arduino-FOC · GitHub

I went with changing t1 and t2 to uint32_t. Speed seemed to be no different compared to keeping them 16-bit and only doing the fraction multiply in 32-bit.

@ChrisMicro

The phase conversion line seems to be problematic for me:

unsigned int i = (unsigned int)(a * (64*4*256.0f/_2PI));

with quite undefined behaviour at large phase values ‘a’.

The theory there is to scale the angle to have 65536 steps per revolution so we can use bitmasking instead of calling _normalizeAngle. Unsigned int should work on any platform since the result is chopped into an 8-bit table index and 8-bit fraction, and int is always at least 16 bits.

At what point are you getting undefined behavior? It may just be float precision trouble, which is a problem for large angles in general. Try calling _normalizeAngle before _sin. It if still fails at the same point, you can be reasonably sure it’s float precision.