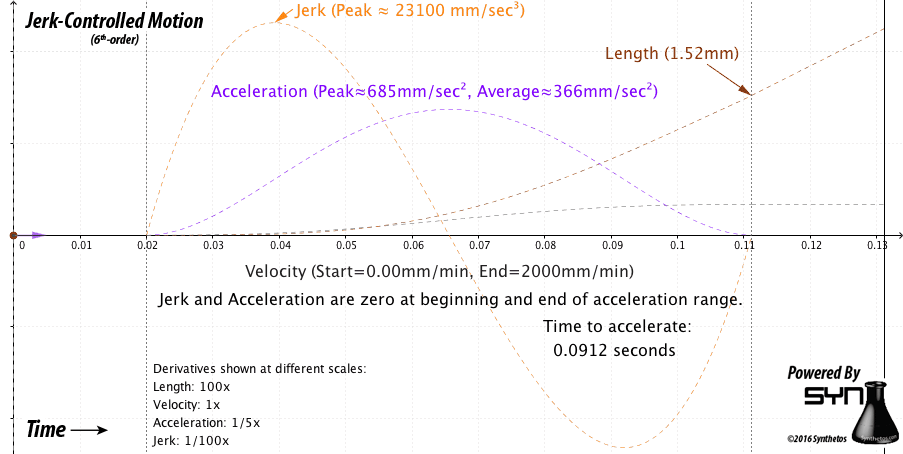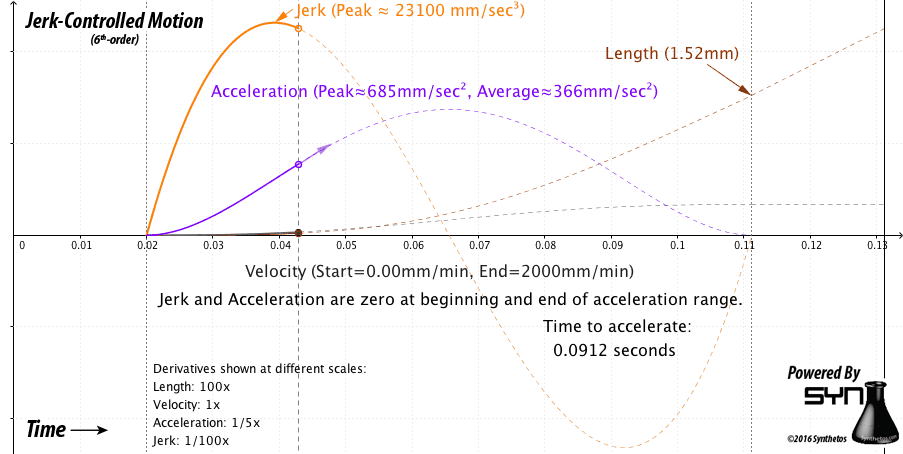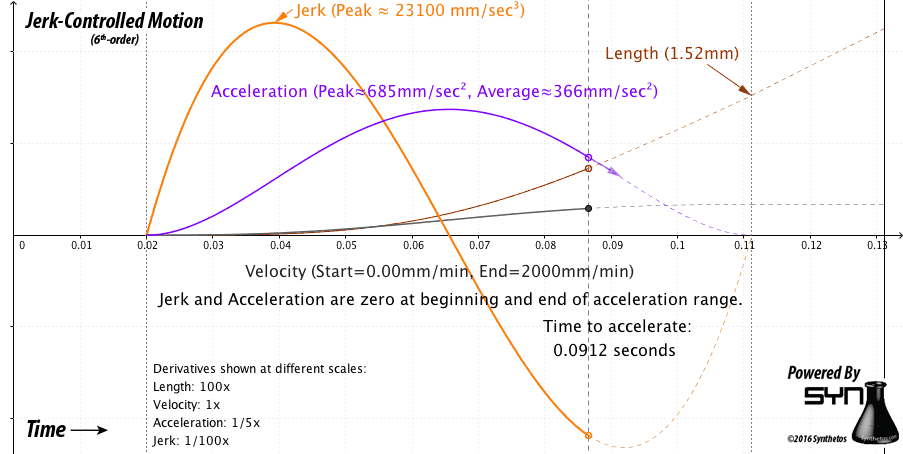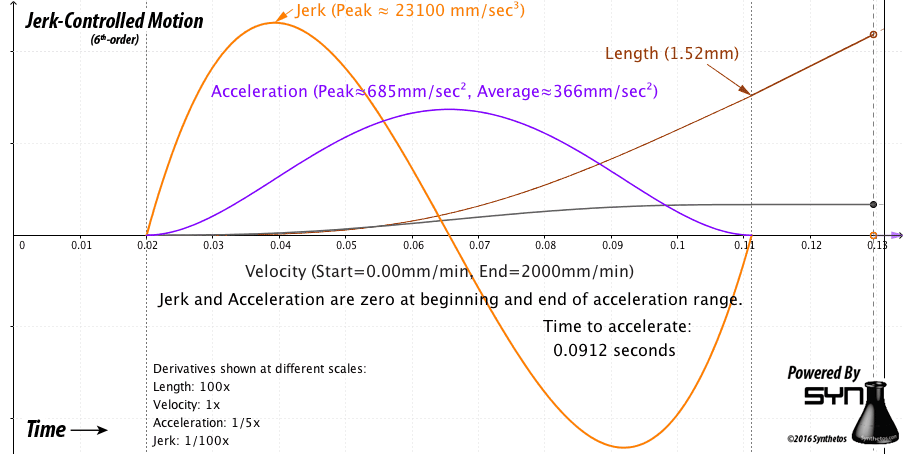
Making progress here with that post from @JorgeMaker regarding the Trapezoidal Path Planner. This algorithm does seem to be able to generate the position the SimpleFOC device should be at for any arbitrary time and calculates that position based on an acceleration / deceleration profile.
I’ve heavily tweaked the Python code (ODrive/tools/motion_planning/PlanTrap.py at a8461c40fd6d97991adc9d553db3fdbce4a01dc4 · odriverobotics/ODrive · GitHub) and this is exactly what I need for giving SimpleFOC the positions each time through the loop (or each N times through the loop).
As an example, here’s a typical move I’d make on the robot arm. I’d go from position 0 (radians) to position 30 (radians, roughly 5 turns of motor). That is shown on the Y axis.
I would make this move very slowly if I’m moving a heavy object. So I would use velocity of 10 radians/second and an acceleration of 5 radians/second/second.
The Python code gives me a perfect acceleration / coast / deceleration profile. It calculates that my total move time is 5 secs. 2 seconds spent accelerating, 1 second in coast, and 2 seconds decelerating.
Start position (rads): 0
End position (rads): 30
Velocity for move (rads/s): 10
Acceleration (rads/s/s): 5
Here is a test of the code that would get called each time through the loop at any arbitrary time to find what the current position should be, so that we can update the position target in SimpleFOC as fast as possible.
t (seconds): 1.00
Acceleration stage
y (pos): 2.50
y_Accel (): 10.00
yd (vel): 5.00
ydd (acc): 5.00
t (seconds): 2.50
Coasting stage
y (pos): 15.00
y_Accel (): 10.00
yd (vel): 10.00
ydd (acc): 0.00
t (seconds): 4.00
Deceleration stage
y (pos): 27.50
y_Accel (): 10.00
yd (vel): 5.00
ydd (acc): -5.00
Here is the code that would get run each time through the loop:
Python Code calc_step_pos_at_arbitrary_time()
def calc_step_pos_at_arbitrary_time(t, Xf, Xi, Vi, Ar, Vr, Dr, Ta, Tv, Td, Tf):
# t is the current time
# t would be calculated based on microseconds() passed
# since the start of the current move
#t = 4.5
# We only know acceleration (Ar and Dr), so we integrate to create
# the velocity and position curves
# we should do this once at the start of the move, not
# each time thru this step method
y_Accel = Xi + Vi*Ta + 0.5*Ar*Ta**2
y = None
yd = None
ydd = None
print()
print("t (seconds): {:.2f}".format(t))
if t < 0: # Initial conditions
print("Initial conditions")
y = Xi
yd = Vi
ydd = 0
elif t < Ta: # Acceleration
print("Acceleration stage")
y = Xi + Vi*t + 0.5*Ar*t**2
yd = Vi + Ar*t
ydd = Ar
elif t < Ta+Tv: # Coasting
print("Coasting stage")
y = y_Accel + Vr*(t-Ta)
yd = Vr
ydd = 0
elif t < Tf: # Deceleration
print("Deceleration stage")
td = t-Tf
y = Xf + 0*td + 0.5*Dr*td**2
yd = 0 + Dr*td
ydd = Dr
elif t >= Tf: # Final condition
print("Final condition")
y = Xf
yd = 0
ydd = 0
else:
raise ValueError("t = {} is outside of considered range".format(t))
print("y (pos): {:.2f}".format(y))
print("y_Accel (): {:.2f}".format(y_Accel))
print("yd (vel): {:.2f}".format(yd))
print("ydd (acc): {:.2f}".format(ydd))
return (y, yd, ydd)
Then, just to test the algorithm further, let’s decrease the acceleration to 2 radians/sec/sec, which is slow enough where we may never get to a coast phase because we reach our final destination before the maximum velocity of 10 radians/sec can be achieved.
Start position (rads): 0
End position (rads): 30
Velocity for move (rads/s): 10
Acceleration (rads/s/s): 2
This time it takes us 7.74 seconds to reach our destination. 3.87 on accelerate and 3.87 on decelerate. We never reach coast, so we have a triangle shape move rather than a trapezoidal shape.
Thus this algorithm is going to do the job for us. Here’s the main calculation code that would get run once at the start of the move:
Python Code calc_plan_trapezoidal_path_at_start()
def calc_move_parameters_at_start(Xf, Xi, Vi, Vmax, Amax, Dmax):
dX = Xf - Xi # Distance to travel
stop_dist = Vi**2 / (2*Dmax) # Minimum stopping distance
dXstop = np.sign(Vi)*stop_dist # Minimum stopping displacement
s = np.sign(dX - dXstop) # Sign of coast velocity (if any)
Ar = s*Amax # Maximum Acceleration (signed)
Dr = -s*Dmax # Maximum Deceleration (signed)
Vr = s*Vmax # Maximum Velocity (signed)
# If we start with a speed faster than cruising, then we need to decel instead of accel
# aka "double deceleration move" in the paper
if s*Vi > s*Vr:
print("Handbrake!")
Ar = -s*Amax
# Time to accel/decel to/from Vr (cruise speed)
Ta = (Vr-Vi)/Ar
Td = -Vr/Dr
# Integral of velocity ramps over the full accel and decel times to get
# minimum displacement required to reach cruising speed
dXmin = Ta*(Vr+Vi)/2.0 + Td*(Vr)/2.0
# Are we displacing enough to reach cruising speed?
if s*dX < s*dXmin:
print("Short Move:")
# From paper:
# Vr = s*math.sqrt((-(Vi**2/Ar)-2*dX)/(1/Dr-1/Ar))
# Simplified for less divisions:
Vr = s*math.sqrt((Dr*Vi**2 + 2*Ar*Dr*dX) / (Dr-Ar))
Ta = max(0, (Vr - Vi)/Ar)
Td = max(0, -Vr/Dr)
Tv = 0
else:
print("Long move:")
Tv = (dX - dXmin)/Vr # Coasting time
Tf = Ta+Tv+Td
print("Xi: {:.2f}\tXf: {:.2f}\tVi: {:.2f}".format(Xi, Xf, Vi))
print("Amax: {:.2f}\tVmax: {:.2f}\tDmax: {:.2f}".format(Amax, Vmax, Dmax))
print("dX: {:.2f}\tdXst: {:.2f}\tdXmin: {:.2f}".format(dX, dXstop, dXmin))
print("Ar: {:.2f}\tVr: {:.2f}\tDr: {:.2f}".format(Ar, Vr, Dr))
print("Ta: {:.2f}\tTv: {:.2f}\tTd: {:.2f}".format(Ta, Tv, Td))
return (Ar, Vr, Dr, Ta, Tv, Td, Tf)
Here is the final code that now needs to be transposed to C code for running with SimpleFOC. I think I’ll add a commander command like G for Gcode and have users submit something like “G30 V10 A5” for move 30 radians at velocity of 10 (rads/s) at acceleration of 5 (rads/s/s).
# Copyright (c) 2021 John Lauer for modifications
#
# Original copyrights and code by
# Original URL https://github.com/odriverobotics/ODrive/blob/a8461c40fd6d97991adc9d553db3fdbce4a01dc4/tools/motion_planning/PlanTrap.py
# Copyright (c) 2018 Paul Guénette
# Copyright (c) 2018 Oskar Weigl
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
# The above copyright notice and this permission notice shall be included in all
# copies or substantial portions of the Software.
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
# SOFTWARE.
# This algorithm is based on:
# FIR filter-based online jerk-constrained trajectory generation
# https://www.researchgate.net/profile/Richard_Bearee/publication/304358769_FIR_filter-based_online_jerk-controlled_trajectory_generation/links/5770ccdd08ae10de639c0ff7/FIR-filter-based-online-jerk-controlled-trajectory-generation.pdf
def calc_plan_trapezoidal_path_at_start(Xf, Xi, Vi, Vmax, Amax, Dmax):
dX = Xf - Xi # Distance to travel
stop_dist = Vi**2 / (2*Dmax) # Minimum stopping distance
dXstop = np.sign(Vi)*stop_dist # Minimum stopping displacement
s = np.sign(dX - dXstop) # Sign of coast velocity (if any)
Ar = s*Amax # Maximum Acceleration (signed)
Dr = -s*Dmax # Maximum Deceleration (signed)
Vr = s*Vmax # Maximum Velocity (signed)
# If we start with a speed faster than cruising, then we need to decel instead of accel
# aka "double deceleration move" in the paper
if s*Vi > s*Vr:
print("Handbrake!")
Ar = -s*Amax
# Time to accel/decel to/from Vr (cruise speed)
Ta = (Vr-Vi)/Ar
Td = -Vr/Dr
# Integral of velocity ramps over the full accel and decel times to get
# minimum displacement required to reach cruising speed
dXmin = Ta*(Vr+Vi)/2.0 + Td*(Vr)/2.0
# Are we displacing enough to reach cruising speed?
if s*dX < s*dXmin:
print("Short Move:")
# From paper:
# Vr = s*math.sqrt((-(Vi**2/Ar)-2*dX)/(1/Dr-1/Ar))
# Simplified for less divisions:
Vr = s*math.sqrt((Dr*Vi**2 + 2*Ar*Dr*dX) / (Dr-Ar))
Ta = max(0, (Vr - Vi)/Ar)
Td = max(0, -Vr/Dr)
Tv = 0
else:
print("Long move:")
Tv = (dX - dXmin)/Vr # Coasting time
Tf = Ta+Tv+Td
# We only know acceleration (Ar and Dr), so we integrate to create
# the velocity and position curves
# we should do this once at the start of the move, not
# each time thru this step method
y_Accel = Xi + Vi*Ta + 0.5*Ar*Ta**2
print("Xi: {:.2f}\tXf: {:.2f}\tVi: {:.2f}".format(Xi, Xf, Vi))
print("Amax: {:.2f}\tVmax: {:.2f}\tDmax: {:.2f}".format(Amax, Vmax, Dmax))
print("dX: {:.2f}\tdXst: {:.2f}\tdXmin: {:.2f}".format(dX, dXstop, dXmin))
print("Ar: {:.2f}\tVr: {:.2f}\tDr: {:.2f}".format(Ar, Vr, Dr))
print("Ta: {:.2f}\tTv: {:.2f}\tTd: {:.2f}".format(Ta, Tv, Td))
print("y_Accel: {:.2f}".format(y_Accel))
print("Tf (full move time): {:.2f}".format(Tf))
return (Ar, Vr, Dr, Ta, Tv, Td, Tf, y_Accel)
def calc_step_pos_at_arbitrary_time(t, Xf, Xi, Vi, Ar, Vr, Dr, Ta, Tv, Td, Tf, y_Accel):
# t is the current time
# t would be calculated based on microseconds() passed
# since the start of the current move
#t = 4.5
y = None
yd = None
ydd = None
print()
print("t (seconds): {:.2f}".format(t))
if t < 0: # Initial conditions
print("Initial conditions")
y = Xi
yd = Vi
ydd = 0
elif t < Ta: # Acceleration
print("Acceleration stage")
y = Xi + Vi*t + 0.5*Ar*t**2
yd = Vi + Ar*t
ydd = Ar
elif t < Ta+Tv: # Coasting
print("Coasting stage")
y = y_Accel + Vr*(t-Ta)
yd = Vr
ydd = 0
elif t < Tf: # Deceleration
print("Deceleration stage")
td = t-Tf
y = Xf + 0*td + 0.5*Dr*td**2
yd = 0 + Dr*td
ydd = Dr
elif t >= Tf: # Final condition
print("Final condition")
y = Xf
yd = 0
ydd = 0
else:
raise ValueError("t = {} is outside of considered range".format(t))
print("y (pos): {:.2f}".format(y))
print("y_Accel (): {:.2f}".format(y_Accel))
print("yd (vel): {:.2f}".format(yd))
print("ydd (acc): {:.2f}".format(ydd))
return (y, yd, ydd)
if __name__ == '__main__':
Xf = 30 # Position we're moving to (rads)
Xi = 0 # Initial position (rads)
Vi = 0 # Initial velocity (rads/s)
Vmax = 10 # Velocity max (rads/s)
Amax = 5 # Acceleration max (rads/s/s)
Dmax = Amax # Decelerations max (rads/s/s)
# Plan the path
(Ar, Vr, Dr, Ta, Tv, Td, Tf, y_Accel) = calc_plan_trapezoidal_path_at_start(Xf, Xi, Vi, Vmax, Amax, Dmax)
# Example calls each time through loop during move
# Time = 1 second
(Y, Yd, Ydd) = calc_step_pos_at_arbitrary_time(1, Xf, Xi, Vi, Ar, Vr, Dr, Ta, Tv, Td, Tf, y_Accel)
# Time = 2.5 seconds
(Y, Yd, Ydd) = calc_step_pos_at_arbitrary_time(2.5, Xf, Xi, Vi, Ar, Vr, Dr, Ta, Tv, Td, Tf, y_Accel)
# Time = 4 seconds
(Y, Yd, Ydd) = calc_step_pos_at_arbitrary_time(4, Xf, Xi, Vi, Ar, Vr, Dr, Ta, Tv, Td, Tf, y_Accel)